درخت تصمیم‌گیری در یادگیری ماشین چیست و چه کاربردی دارد؟

درخت تصمیم چیست؟

الگوریتم درخت تصمیم یک الگوریتم یادگیری ماشین تحت نظارت محبوب است که به دلیل رویکرد ساده‌ای که دارد گزینه مناسبی برای کار با مجموعه داده‌های پیچیده است. دلیل نام‌گذاری درخت‌های تصمیم‌گیری شباهت عملکردی آن‌ها به ریشه‌ها، شاخه‌ها و برگ‌ها یک درخت است که در قالب گره‌ها و لبه‌ها خود را نشان می‌دهد. آن‌ها برای تجزیه و تحلیل تصمیم‌ها عملکردی مشابه با نمودارهای جریانی دارند که مبتنی بر الگوی «اگر» است. درخت این قوانین تصمیم‌گیری if-else را می‌آموزد تا مجموعه داده‌ها را برای ایجاد یک مدل درخت تقسیم‌بندی کند.

درخت‌های تصمیم‌گیری به شکل گسترده‌ای در پیش‌بینی نتایج گسسته، مسائل طبقه‌بندی و نتایج عددی پیوسته برای مسائل رگرسیونی مورد استفاده قرار می‌گیرند. الگوریتم‌های مختلفی در این زمینه وجود دارند که از آن جمله باید به CART، C4.5 و مجموعه‌هایی مانند جنگل‌های تصادفی و درختان تقویت‌شده گرادیان توسعه اشاره کرد.

الگوریتم درخت تصمیم در دسته یادگیری تحت نظارت قرار می‌گیرد و می‌توان از آن‌ها برای حل مسائل رگرسیون (regression) و طبقه‌بندی (classification) استفاده کرد. درخت تصمیم از نمایش درختی برای حل این مشکل استفاده می کند که در آن هر گره برگ با یک برچسب کلاس مطابقت دارد و ویژگی‌ها در گره داخلی درخت نشان داده می‌شوند. ما می‌توانیم هر تابع بولی را روی ویژگی‌های گسسته با استفاده از درخت تصمیم نمایش دهیم. شکل زیر این مسئله را نشان می‌دهد.

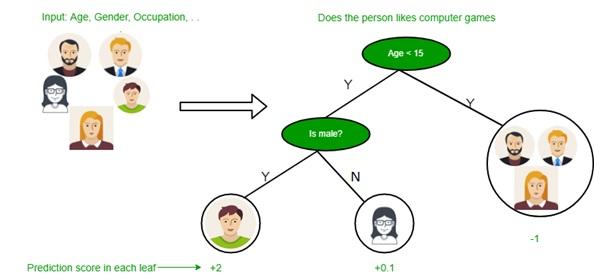
در ابتدا کل مجموعه آموزشی را ریشه در نظر می‌گیریم.

مقادیر ویژگی که ارزش بیشتری دارند را به دسته‌بندی اضافه می‌کنیم. در این حالت اگر مقادیر پیوسته باشند، قبل از ساخت مدل گسسته می‌شوند.

بر اساس مقادیر ویژگی، رکوردها به صورت بازگشتی توزیع می‌شوند.

ما از روش‌های آماری برای مرتب کردن صفات به عنوان ریشه یا گره داخلی استفاده می‌کنیم.

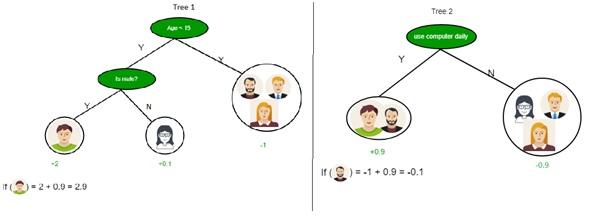
کاربرد  درخت تصمیم‌‌گیری در حوزه یادگیری ماشین

همان‌گونه که اشاره شد، درخت تصمیم‌گیری، مکانیزمی برای شکل‌دهی یا سازمان‌دهی به الگوریتمی است که قرار است برای ساخت یک مدل یادگیری ماشین از آن استفاده شود. الگوریتم درخت تصمیم‌‌گیری برای تقسیم ویژگی‌های مجموعه داده‌ها با استفاده از تابع هزینه (Cost Function) استفاده می‌شود. نکته مهمی که باید به آن دقت کنید این است که الگوریتم قبل از آن‌که عملی برای بهینه‌سازی و حذف شاخه‌های اضافی انجام دهد، به‌شکلی رشد می‌کند که ویژگی‌های غیرمرتبط با مسئله را نشان می‌دهد. به همین دلیل، عملیات هرس کردن (Pruning) برای حذف شاخه‌های اضافه انجام می‌شود. درست مشابه با دنیای واقعی که شاخه‌های درختان هرس می‌شود. در الگوریتم درخت تصمیم‌گیری، این امکان وجود دارد تا پارامترهایی مثل عمق درخت تصمیم را تنظیم کرد تا مشکلات بیش‌برازش (Overfitting) و پیچیدگی بیش‌از‌حد درخت به کمترین مقدار برسد. 

امروزه انواع مختلفی از درخت‌های تصمیم‌گیری در حوزه یادگیری ماشین برای مسائل طبقه‌بندی اشیاء بر‌ اساس ویژگی‌های آموزش‌داد‌شده، مورد استفاده قرار می‌گیرند. جالب آن‌که برنامه‌نویسان یادگیری ماشین از درخت‌های تصمیم‌ در مسائل رگرسیون یا پیش‌بینی نتایج پیوسته داده‌های دیده‌نشده نیز استفاده می‌کنند. درخت‌های تصمیم با ارائه یک دید بصری و قابل درک، روند تصمیم‌گیری را ساده کرده و فرآیند توسعه مدل‌های یادگیری ماشین را شتاب می‌بخشند. تنها نکته منفی که در مورد درخت‌های تصمیم وجود دارد این است که با زیاد شدن تعداد شاخه‌های درخت، فرآیند درک و استفاده از آن به‌دلیل پیچیدگی بیش‌از‌حد درخت، سخت می‌شود؛ از این‌رو، هرس تکنیکی است که باید در مورد درخت‌ها از آن استفاده کرد. در مجموع باید بگوییم درخت تصمیم راهکاری ساختاریافته برای مصورسازی تصمیم‌ها، مدل‌سازی آن‌ها و دریافت خروجی‌های دقیق است، به‌طوری که میزان موفقیت گزینه‌ها (تصمیم‌ها) در دستیابی به یک هدف خاص را نشان می‌دهد. 

مطلب پیشنهادی

سازمان‌دهی و مرتب‌سازی سریع داده‌ها

آشنایی با انواع درخت‌ها در ساختمان داده‌ها

آشنایی با چند اصطلاح پرکاربرد درخت‌های تصمیم‌گیری

قبل از آن‌که معماری درخت تصمیم را بررسی کنیم، ابتدا باید اشاره‌ای به چند اصطلاح مهم و پرکاربرد این حوزه داشته باشیم. 

• گره ریشه (Root Node): نشان‌دهنده مجموعه داده‌های مسئله است که به دو یا چند مجموعه همگن (Homogeneous) تقسیم می‌شوند. گره ریشه بالاترین گره درخت تصمیم‌گیری است. 
• تقسیم‌بندی (Splitting): پردازشی است که برای تقسیم گره‌ها به دو یا چند زیرگره انجام می‌شود. 
• گره برگ/انتهایی (Terminal Node): گره‌های انتهایی هر شاخه که امکان تقسیم‌بندی آن‌ها وجود ندارد، گره برگ (Leaf Node) یا گره انتهایی نام دارند. 
• هرس کردن (Pruning): در بیشتر موارد باید بخش‌های زائد از یک درخت حذف شوند. هنگامی که نیاز باشد زیر‌گره‌هایی از گره تصمیم حذف شوند، فرآیند هرس آغاز می‌شود. در حالت کلی باید بگوییم که هرس کردن، عملیاتی در نقطه مقابل تفکیک است. 
• زیردرخت یا شاخه (Branch /Sub-Tree): زیر‌بخش‌های درخت تصمیم، شاخه یا زیردرخت نام دارند. 
• گره والد و فرزند (Parent and Child Node): گره‌ای که به زیرگره‌های دیگر تقسیم می‌شود، گره والد زیرگره‌ها نام دارد. در این حالت گره‌های ساخته‌شده، فرزند آن گره والد نام دارند. 

شکل 1، مفاهیم و اصطلاحات پیرامون درخت تصمیم را نشان می‌دهد. درخت‌های تصمیم‌گیری گره‌های مختلفی دارند. اولین گره، گره ریشه نام دارد که نقطه شروع درخت است که مجموعه داده‌های مسئله را در خود جای می‌دهد. در ادامه، گره‌های برگ قرار دارند که نقطه پایانی هر شاخه درخت یا خروجی نهایی مجموعه‌ای از تصمیم‌ها هستند. هر شاخه درخت تصمیم‌گیری در حوزه یادگیری ماشین تنها یک گره برگ دارد، به‌طوری که ویژگی یا خصلت (Attribute) داده‌ها در گره‌های داخلی شاخه‌‌ها و نتیجه آن‌ها در برگ هر شاخه را نشان می‌دهند. شکل 2، نمایی از یک درخت تصمیم‌گیری را نشان می‌دهد. 

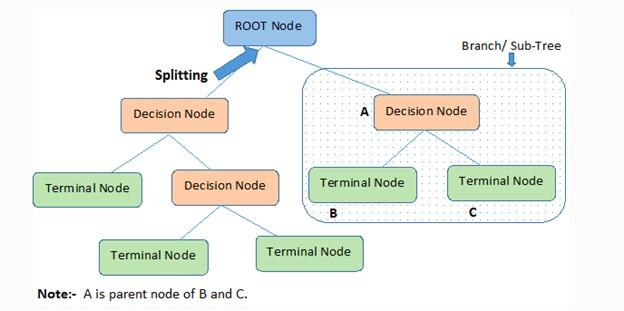
شکل 1

همان‌گونه که در شکل 2 مشاهده می‌کنید، درخت‌های تصمیم با ارائه یک نمای بصری ساده و قابل فهم به برنامه‌نویسان در یافتن بهینه‌ترین راه‌حل کمک می‌کنند. 

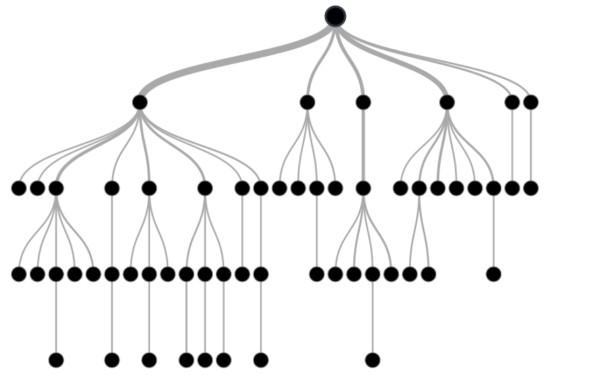
شکل 2

یکی از مفاهیم مهم مرتبط با درخت تصمیم و یادگیری ماشین توضیح‌پذیری (Explainability) است. توضیح‌پذیری به فرآیند توضیح خروجی یک مدل برای افراد فنی و غیرفنی اشاره دارد. خوشبختانه، درخت‌های تصمیم این فرآیند را به‌خوبی پیاده‌سازی می‌کنند. یکی از مهم‌ترین جنبه‌های یادگیری ماشین، بهینه‌سازی وظایف، بدون دخالت و کنترل مستقیم متخصصان است، با این‌حال در بیشتر موارد توضیح خروجی و کاری که یک مدل انجام می‌دهد، سخت است. به همین دلیل، متخصصان یادگیری ماشین از ساختار درختی و شاخه‌های یک درخت برای توضیح هر تصمیمی که یادگیری ماشین اتخاذ می‌کند، استفاده می‌کنند.

مطلب پیشنهادی

آشنایی با انواع مدل‌های یادگیری ماشین

عملکرد درخت تصمیم‌گیری به چه صورتی است؟ 

درختان تصمیم از چند الگوریتم برای تصمیم‌گیری برای تقسیم یک گره به دو یا چند گره فرعی استفاده می‌کنند. تصمیم‌گیری در مورد تقسیم‌های استراتژیک به‌شدت بر دقت و عملکرد درخت تاثیرگذار هستند، به همین دلیل درختان طبقه‌بندی و رگرسیون از سنجه‌های مختلفی برای تصمیم‌گیری استفاده می‌کنند. 

همچنین، درختان تصمیم از چند الگوریتم برای تصمیم‌گیری در مورد تقسیم یک گره به دو یا چند گره فرعی استفاده می‌کنند. جالب آن‌که، فرآیند تقسیم‌بندی و ساخت گره‌های فرعی، همگنی آن‌ها را افزایش می‌دهد. به عبارت دیگر، می‌توان گفت، عملکرد مطلوب یک گره ارتباط مستقیم با متغیر (سنجه) هدفی دارد که استفاده می‌شود. درخت تصمیم، گره‌ها را بر مبنای متغیرهای در دسترس تقسیم می‌کند. 

نکته‌ای که باید به‌عنوان یک مهندس یادگیری ماشین به آن دقت کنید این است که انتخاب الگوریتم بر اساس نوع متغیرهای هدف انجام می‌شود. از الگوریتم‌های مهم قابل استفاده در درخت‌های تصمیم به موارد زیر باید اشاره کرد:

• الگوریتم درخت تصمیم (ID3) که برخی منابع آن‌را Iterative Dichotomiser 3 می‌نامند. الگوریتم ID3 یک درخت چند مسیره بر مبنای رویکرد جست‌وجوی حریصانه ایجاد می‌کند و در ادامه برای هر گره ویژگی گسسته و گروهی را پیدا می‌کند. الگوریتم‌های ID3 در حوزه یادگیری ماشین بیشترین اطلاعات در مورد مسائلی که مبتنی بر اهداف گسسته هستند، ارائه می‌کنند. یک الگوریتم حریصانه، همان‌گونه که از نامش پیدا است، همیشه انتخابی را انجام می‌دهد که در آن لحظه بهترین به‌نظر می‌رسد.
•   الگوریتم پرکاربرد دیگر درخت تصمیم C4.5 نام دارد که جایگزین ID3 شده است. الگوریتم فوق تعریفی پویا برای یک ویژگی گسسته بر مبنای متغیرهای عددی ارائه می‌کند که مقادیر ویژگی پیوسته را به مجموعه‌ای از بخش‌های گسسته تقسیم می‌کنند؛ به‌طوری که محدودیت‌ پیرامون ویژگی‌هایی را که باید حالت گسسته داشته باشند حذف می‌کنند. 
•   الگوریتم درخت تصمیم CART که برخی منابع آن‌را درخت‌های طبقه‌بندی و رگرسیون (Classification and Regression Trees) می‌نامند، شباهت زیادی به الگوریتم C4.5 دارد. تفاوت دو الگوریتم فوق این است که الگوریتم CART از متغیرهای هدف پیوسته و عددی پشتیبانی می‌کند و هیچ محاسبه‌ای روی مجموعه قوانین انجام نمی‌دهد. به بیان دقیق‌تر، الگوریتم از طریق ویژگی و آستانه‌ای که بیشترین مجموعه داده را در یک گره ایجاد می‌کند، درخت دودویی (باینری) را ایجاد می‌کند. 
•    الگوریتم درخت تصمیم CHAID که برخی منابع آن‌را الگوریتم شناسایی اثرات متقابل خودکار کای 2 سرنام Chi-squared Automatic Interaction Detection می‌نامند، در هر گام، از متغیر پیش‌بینی‌کننده که بیشترین تعامل با متغیر وابسته را دارد، در ساخت درخت استفاده می‌کند. الگوریتم فوق، هنگام محاسبه و تقسیم‌بندی درختان چندسطحی از کای 2 استفاده می‌کند. سطوح یا طبقه‌های هر متغیر پیش‌بینی‌کننده ممکن است با یک‌دیگر ادغام شوند تا سطح قابل فهمی ایجاد شود. 
•     الگوریتم درخت تصمیم MARS یا به بیان دقیق‌تر رگرسیون تطبیقی چندمتغیره، الگوریتمی است که برای حل مسائل پیچیده رگرسیون غیرخطی مورد استفاده قرار می‌گیرد. این الگوریتم، جست‌وجویی در مجموعه‌ای از توابع خطی ساده انجام می‌دهد تا بتواند بهترین عملکرد برای پیش‌بینی‌ها را ارائه کند. 

مطلب پیشنهادی

شیوه‌ها و مراحل تصمیم‌گیری

آشنایی با درخت تصمیم‌گیری (Decision Tree)، جنگل تصادفی (Random forest) و بازشناسی الگوها

در درخت تصمیم برای پیش‌بینی کلاس‌های مورد نظر مجموعه داده مسئله، فرآیند محاسبه از گره ریشه آغاز می‌شود. در این حالت، الگوریتم مقادیر ویژگی‌های ریشه را با ویژگی‌های داده‌ها مقایسه و بر اساس این قیاس، شاخه‌ها را دنبال می‌کند و به گره بعدی می‌رود. برای گره بعدی، الگوریتم دومرتبه مقدار ویژگی داده‌ها را با زیرگره‌های دیگر مقایسه می‌کند و روند ساخت درخت را ادامه می‌دهد. این فرآیند تا رسیدن به گره برگ یا همان گره انتهایی درخت ادامه پیدا می‌کند. روند انجام این فرآیندها مرحله‌به‌مرحله به‌شرح زیر است:

• گام اول: الگوریتم درخت تصمیم از گره ریشه کار را آغاز می‌کند که مبتنی بر تمام داده‌ها است.
• گام دوم: بر مبنای مکانیزم سنجش انتخاب ویژگی (ASM) سرنام Attribute Selection Measure ایده‌آل‌ترین ویژگی در مجموعه داده انتخاب می‌شود.
• گام سوم: فرآیند تقسیم گره ریشه به زیرمجموعه‌هایی انجام می‌شود که شامل مقادیر ایده‌آل یا بهترین ویژگی‌ها خواهند بود. 
• گام چهارم: فرآیند ساخت گرهی که ویژگی‌های دقیقی را دارد. 
• گام پنجم: بر مبنای زیرمجموعه‌های طراحی شده، درخت‌های تصمیم جدیدی به‌شکل برگشتی ایجاد می‌شوند. این روند ادامه پیدا می‌کند تا وقتی که امکان دسته‌بندی و تقسیم گره‌ها وجود نداشته باشد. در این حالت، گره نهایی به‌عنوان گره برگ یا انتهایی در نظر گرفته می‌شود. 

مطلب پیشنهادی

یادگیری ماشین با پایتون

چگونه یادگیری ماشین را به عنوان یک فرد تازه‌کار بیاموزیم؟

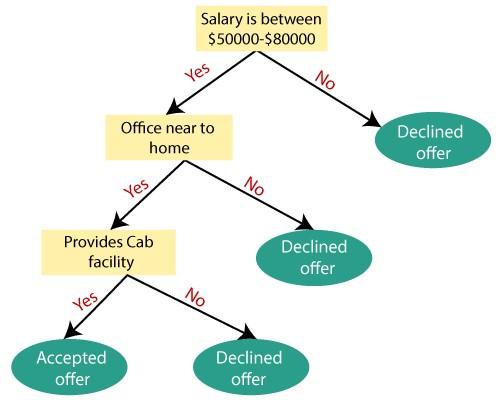
به‌طور مثال، فرض کنید فردی یک پیشنهاد شغلی دارد و قصد دارد بر مبنای مفروضاتی که دارد، این موقعیت شغلی را انتخاب یا رد کند. اگر قرار باشد این مسئله بر مبنای درخت تصمیم حل شود، فرآیند انجام کارها به‌شرح زیر است: 

الگوریتم درخت تصمیم کار را با گره ریشه و ویژگی حقوق (Salary) و بر مبنای سنجش آن ویژگی آغاز می‌کند. در ادامه، گره ریشه به گره تصمیم بعدی که گره مربوط به ویژگی فاصله از شرکت (distance from the office) و یک گره برگ بر مبنای برچسب‌های مربوطه برای رد درخواست پیشنهاد شغلی است، تقسیم می‌شود.

گره‌های تصمیم‌گیرنده بعدی به‌ترتیب به امکانات سازمان و گره رد درخواست پیشنهاد شغلی تقسیم می‌شوند. در نهایت، گره تصمیم به دو گره برگ یعنی پذیرش پیشنهاد شغلی (Accepted offers) و رد پیشنهاد شغلی (Declined offer) تقسیم می‌شود. شکل 3، روند ساخت درخت بر مبنای توضیحاتی که ارائه کردیم را نشان می‌دهد. 

شکل 3

سنجش انتخاب ویژگی (Attribute Selection Measures)

در هنگام طراحی و پیاده‌سازی درخت تصمیم، موضوع مهمی که باید به آن دقت کنید انتخاب بهترین ویژگی برای گره ریشه و گره‌های فرعی است. برای این مسئله، راه‌حلی که «سنجش انتخاب ویژگی» (Attribute Selection Measure) نام دارد، مورد استفاده قرار می‌گیرد. با روش فوق می‌توان بهترین ویژگی را برای گره ریشه و دیگر گره‌های درخت انتخاب کرد. روش سنجش انتخاب ویژگی بر مبنای دو تکنیک زیر پیاده‌سازی می‌شود: 

•   به‌دست آوردن اطلاعات (Information Gain)
•   شاخص جینی (Gini Index)

به‌دست آوردن اطلاعات چیست؟

به‌دست آوردن اطلاعات، به‌معنای جمع‌آوری داده‌ها از طریق سنجش تغییرات، همراه با ناخالصی (آنتروپی) پس از تقسیم‌بندی یک مجموعه داده بر اساس ویژگی‌ها است.وقتی از یک گره در درخت تصمیم استفاده می‌کنیم تا نمونه‌های آموزشی را به زیر مجموعه‌های کوچک‌تر تقسیم کنیم، آنتروپی تغییر می‌کند. افزایش اطلاعات معیاری برای این تغییر در آنتروپی است. روش فوق به ارزیابی این مسئله می‌پردازد که یک ویژگی چقدر اطلاعات درباره یک کلاس دارد. بر مبنای مقادیر به‌دست‌آمده، فرآیند تقسیم گره‌ها انجام شده و درخت تصمیم ساخته می‌شود. الگوریتم درخت تصمیم همواره سعی می‌کند بیشترین اطلاعات را به‌دست آورد. در ادامه، اقدام به تقسیم گره‌ای می‌کند که بیشترین اطلاعات را دارد. در روش فوق اطلاعات بر مبنای فرمول زیر به‌دست می‌آیند: 

Information Gain= Entropy(S)- [(Weighted Avg) *Entropy(each feature)  

آنتروپی، سنجه‌ای برای اندازه‌گیری ناخالصی در یک ویژگی مشخص است که تصادفی بودن داده‌ها را نیز مشخص می‌کند. آنتروپی معیار عدم قطعیت یک متغیر تصادفی است، ناخالصی مجموعه‌ای دلخواه از مثال‌ها را مشخص می‌کند. هر چه آنتروپی بیشتر باشد محتوای اطلاعات بیشتر است.معیار فوق بر مبنای فرمول زیر محاسبه می‌شود:

Entropy(s)= -P(yes)log2 P(yes)- P(no) log2 P(no)

• در فرمول بالا S: تعداد همه نمونه‌ها است.
• P(yes): نشان‌دهنده احتمال وقوع پاسخ مثبت است. 
• P(no): نشان‌دهنده احتمال وقوع پاسخ منفی است.

هنگامی که قصد ساخت درخت تصمیم با استفاده از اطلاعات را دارید باید به موارد زیر دقت کنید:

کار را با تمام نمونه‌های آموزشی مرتبط با گره ریشه شروع کنید.

از اطلاعات به دست آمده برای انتخاب ویژگی برای برچسب‌گذاری هر گره استفاده کنید. البته به این نکته دقت کنید که هیچ مسیر ریشه به برگ نباید دو بار دارای همان ویژگی گسسته باشد.

هر زیردرخت را به صورت بازگشتی بر روی زیرمجموعه‌ای از نمونه‌های آموزشی بسازید که در آن مسیر در درخت طبقه‌بندی می‌شوند.

اگر تمام نمونه‌های آموزشی مثبت یا منفی باقی می‌مانند، آن گره را مطابق با «بله» یا «نه» برچسب بزنید.

اگر هیچ ویژگی باقی نماند، نمونه‌های آموزشی که در آن گره باقی مانده‌اند را برچسب بزنید.

اگر نمونه‌ای باقی نماند، نمونه‌های آموزشی والدین را برچسب بزنید.

اکنون، اجازه دهید با استفاده از روش Information gain، یک درخت تصمیم برای داده‌های زیر ترسیم کنیم.

مجموعه آموزشی: 3 ویژگی و 2 کلاس

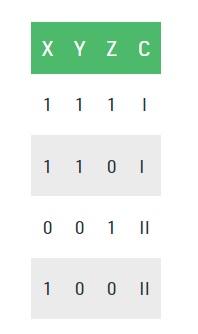
در اینجا، ما 3 ویژگی و 2 کلاس خروجی داریم که برای ساخت آن از اطلاعات به دست آمده استفاده کردیم. ما هر یک از ویژگی‌ها را دریافت می‌کنیم و اطلاعات مربوط به هر ویژگی را محاسبه می‌کنیم.

تقسیم روی ویژگی X

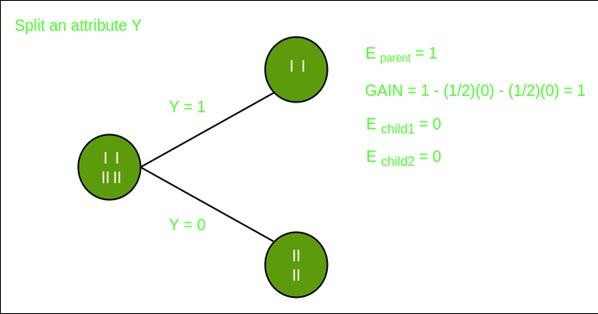
تقسیم روی ویژگی Y

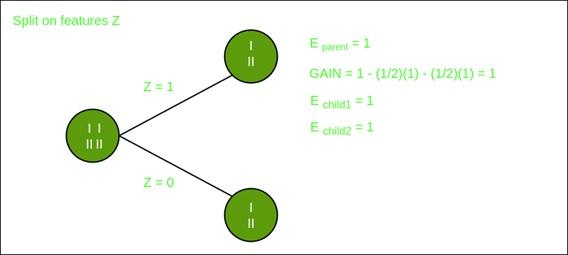
شاخص جینی چیست؟

شاخص جینی معیار اندازه‌گیری تعداد دفعات نادرست شناسایی یک عنصر تصادفی انتخاب شده است در مجموعه داده‌های به‌دست‌آمده است هنگام ساخت درخت تصمیم با الگوریتم CART است. در این حالت، ویژگی با میزان شاخص جینی پایین در درخت تصمیم باید انتخاب شود. از این شاخص تنها برای ساخت طبقه و گروه‌های دودویی استفاده می‌شود. شاخص جینی بر مبنای فرمول زیر محاسبه می‌شود:

Gini Index= 1- ∑jPj2

مجموعه داده در تصویر زیر را در نظر بگیرید تا یک درخت تصمیم را با استفاده از شاخص جینی رسم کنیم.

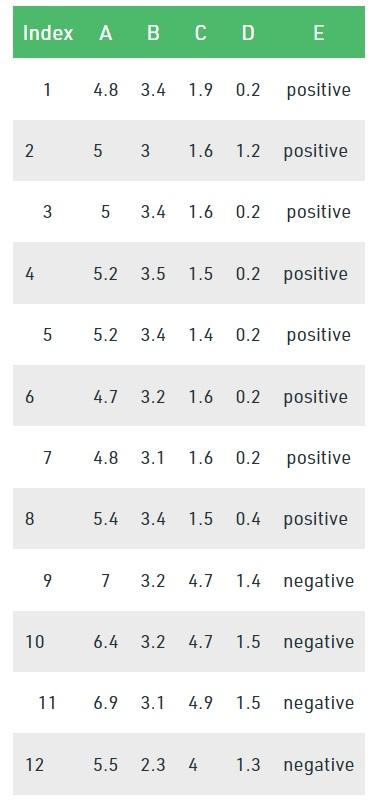
در مجموعه داده بالا 5 ویژگی وجود دارد که ویژگی E ویژگی پیش‌بینی است که شامل 2 کلاس (مثبت و منفی) است. برای هر دو کلاس نسبت مساوی داریم. در شاخص جینی ما باید مقادیر تصادفی را برای دسته‌بندی هر ویژگی انتخاب کنیم. این مقادیر برای این مجموعه داده عبارتند از:

محاسبه شاخص جینی برای A به شرح زیر است:

محاسبه شاخص جینی برای B به شرح زیر است:

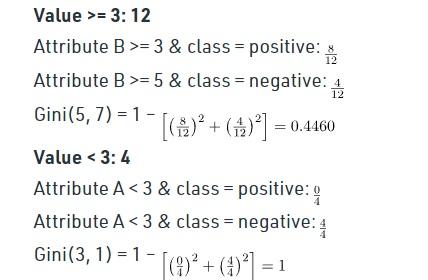
محاسبه شاخص جینی برای C و D به شرح زیر است:

اکنون درخت فوق به شرح زیر است:

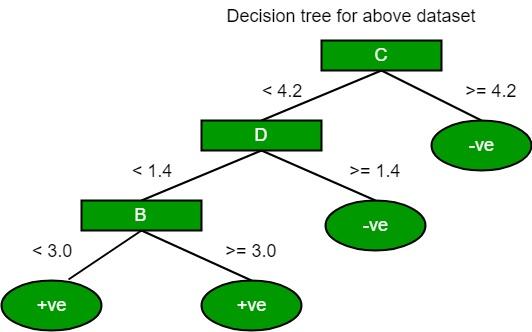
تقسیم دودویی بازگشت درخت تصمیم چیست؟

به طور کلی، ساخت یک درخت تصمیم دودویی در واقع فرآیندی برای تقسیم فضای ورودی است. یک رویکرد حریصانه برای تقسیم فضا به نام تقسیم باینری بازگشتی استفاده می شود. یک روش عددی است که در آن تمام مقادیر در یک ردیف قرار می گیرند و نقاط تقسیم مختلف با استفاده از تابع هزینه آزمایش می‌شوند. در روش تقسیم دودویی، بخش‌های مختلف درخت به‌همراه ویژگی‌های مشخص شده و نقاط تقسیم مختلف با استفاده از تابع هزینه ارزیابی می‌شوند تا بتوان ابعاد درخت را کم کرد. در روش فوق، کمترین هزینه انتخاب می‌شود. روش کار به این صورت است که در انشعاب (Split) اول که ریشه درخت نام دارد، همه ویژگی‌ها در نظر گرفته می‌شوند و داده‌های آموزشی بر مبنای ریشه به گروه‌هایی تقسیم می‌شوند. در ادامه، بخشی که کمترین هزینه را دارد انتخاب می‌شود. بد نیست بدانید که مکانیزم تقسیم دودویی، رویکرد بازگشتی و حریصانه دارد، زیرا گروه‌های تشکیل‌شده را می‌توان از طریق یک استراتژی ساده به گروه‌های کوچک‌تر تقسیم کرد و خود الگوریتم نیز تمایل زیادی برای کاهش هزینه‌ها دارد. در چنین شرایطی، همواره گره ریشه به‌عنوان بهترین پیش‌بینی‌کننده در نظر گرفته می‌شود. 

هزینه تقسیم چگونه محاسبه می‌شود؟ 

تابع هزینه‌ (Cost Function) نقش مهمی در مسائل طبقه‌بندی و رگرسیون دارد. در هر دو حالت، تابع هزینه سعی می‌کند تا شاخه‌های همگن یا شاخه‌هایی با گروه‌هایی از ویژگی‌ها با نتایج مشابه را پیدا کند. فرمول تابع هزینه در ارتباط با مسائل رگرسیون به‌شرح زیر است:

Regression : sum(y — prediction)²

به‌طور مثال، فرض کنید قصد پیش‌بینی قیمت مسکن را داریم. در این حالت، درخت تصمیم با در نظر گرفتن ویژگی‌های تعریف‌شده در داده‌های آموزشی فرآیند تقسیم را آغاز می‌کند. به‌طوری که میانگین نتایج ورودی داده‌های آموزشی یک گروه خاص به‌عنوان معیار پیش‌بینی برای آن گروه در نظر گرفته می‌شود. در این حالت، تابع فوق برای همه نقاط داده در نظر گرفته می‌شود تا کاندیدهای مناسب را پیدا کند. در ادامه، انشعابی که کمترین هزینه را دارد، انتخاب می‌شود. متخصصان یادگیری ماشین در مسائل طبقه‌بندی، از فرمول زیر استفاده می‌کنند: 

Classification : G = sum(pk * (1 — pk))

در این‌جا از معیاری که امتیاز جینی (Gini Score) نام دارد، استفاده می‌شود که میزان خوب و مناسب بودن یک تقسیم از طریق ترکیب پاسخ و نتایج کلاس‌ها در گروه‌های ساخته‌شده با تقسیم‌بندی را نشان می‌دهد. در فرمول بالا، متغیرpk  مقدار ورودی‌های کلاس یکسان را نشان می‌دهد. در این‌جا یک کلاس خالص (Pure) زمانی ساخته می‌شود که یک گروه همه ورودی‌های کلاس را داشته باشد. در این‌جا، مقدار pk  برابر با صفر یا یک، و  G برابر با صفر است. 

کلام آخر

با خواندن این مقاله به پرسش مهمی می‌رسیم که چرا درخت‌های تصمیم استفاده می‌شوند؟ الگوریتم‌های مختلفی در حوزه یادگیری ماشین وجود دارند، به همین دلیل، انتخاب بهترین الگوریتم برای مجموعه داده‌ها یک چالش جدی است. اگر مدلی که قصد طراحی آن‌را دارید بر مبنای یک الگوریتم با عملکرد پایین توسعه پیدا کند، مدل ممکن است با سرعت کمی اقدام به پردازش اطلاعات کند یا نتایج اشتباه زیادی را ارائه کند. به همین دلیل از درخت‌های تصمیم استفاده می‌کنیم. به‌طور کلی، درخت‌های تصمیم به دو دلیل زیر انتخاب می‌شوند:

• در بیشتر موارد، درختان تصمیم سعی در تقلید از تفکر انسانی در تصمیم‌گیری‌ها دارند، بنابراین درک آن‌ها آسان است.
•  منطق پشت درخت تصمیم را می‌توان به‌راحتی درک کرد، زیرا ساختاری همانند درخت‌های واقعی دارند.