آشنایی با انواع درخت‌ها در ساختمان داده‌ها

چه متخصصانی باید با اصول ساختمان داده‌ها آشنا باشند؟

به‌طور کلی، آشنایی با ساختمان داده‌ها برای دانشمندان داده‌، مهندسان داده، متخصصان داده‌کاوی، متخصصان یادگیری ماشین و برنامه‌نویسان ضروری است. نزدیک به نیم قرن است که مهندسان نرم‌افزار به روش‌های مختلف با ساختارهای داده‌ای در ارتباط هستند. بنابراین در مباحثی مثل داده‌کاوی، یادگیری ماشین و برنامه‌نویسی باید شناخت دقیقی در ارتباط با ساختمان داده‌ها داشته باشید. سازمان‌دهی داده‌ها چیست؟ سازمان‌دهی داده‌ها به معنای به‌کارگیری یک روش خاص و بر پایه مدل منطقی یا ریاضی است که برای استفاده بهینه از داده‌ها استفاده می‌شود. ساختار داده‌ها انواع گوناگونی دارد که هر کدام برای کاربرد خاصی استفاده می‌شوند. نکته مهمی که باید به آن دقت کنید تفاوت ساختار داده‌ها و الگوریتم است. ساختار داده‌ها به روش‌های ذخیره‌سازی داده‌ها در کامپیوتر با هدف دسترسی آسان‌تر و بهینه‌تر اشاره دارد، در حالی‌که الگوریتم روشی برای حل مسئله به وسیله کامپیوتر است. 

کدامیک از سرفصل‌های ساختمان داده‌ها ارزش بیشتری دارد؟

پاسخ روشنی برای این پرسش وجود ندارد، زیرا هر یک از موضوعات ساختمان داده برای حل مسئله‌ای خاص استفاده می‌شوند. با این‌حال، برخی از ساختارهای داده‌ای به‌شکل گسترده‌تری در پروژه‌های برنامه‌نویسی استفاده می‌شوند که از مهم‌ترین آن‌ها باید به آرایه (Array)، پشته (Stacks)، صف (Queue)، فهرست پیوندی (Linked List)، درخت (Tree)، گراف (Graph)، درخت پیشوندی (Trie) و جدول درهم‌سازی (Hash Table) اشاره کرد. در این میان درخت‌ها جایگاه خاصی دارند که موضوع این مقاله هستند. 

درخت چیست؟

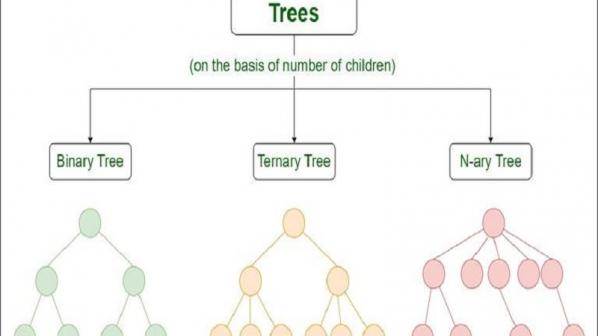
درخت (Tree) یک ساختار داده سلسله مراتبی است که شامل راس‌ها (گره‌ها) و یال‌هایی است که آن‌ها را به یکدیگر متصل می‌کند. درخت‌ها عملکردی شبیه به گراف‌ها دارند، با این تفاوت که درخت‌ها برخلاف گراف، چرخه (Cycle) ندارند. درخت‌ها کاربرد گسترده‌ای در دنیای هوش مصنوعی و الگوریتم‌های هوشمند دارند و راهکاری هوشمند برای ذخیره‌سازی داده‌ها و حل موثر مسائل استفاده می‌کنند. به‌طور مثال، تمامی بازی‌های شطرنجی که انجام می‌دهید، همگی بر مبنای درخت‌ها ساخته شده‌اند. درخت‌ها انواع مختلفی دارند که از آن جمله باید به درخت N-ary، درخت متوازن (Balanced Tree)، درخت دودویی (Binary Tree)، درخت جست‌و‌جوی دودویی (Binary Search Tree)، درخت ای‌وی‌ال (درخت با ارتفاع متوازن | AVL Tree)،درخت سرخ – سیاه (Red Black Tree) و درخت ۲-۳ اشاره کرد. نکته‌ای که خیلی از کاربران فضای مجازی اطلاعی در مورد آن ندارند، کاربرد درخت در یکی از پیچیده‌ترین و خلاقه‌ترین فناوری‌هایی است که این روزها زیاد در مورد آن می‌شنویم. درخت‌ها نقش کلیدی و تعیین‌کننده‌ای در فناوری زنجیره بلوکی دارند. بد نیست بدانید، اولین تلاش برای ساخت زنجیره بلوکی رمزنگاری شده در سال 1991 توسط استوارت هابر و اسکات استورنتا از کارشناسان حوزه رمزنگاری انجام شد. آن‌ها بر مبنای درخت درهم‌ساز موفق به جمع‌آوری چند سند در یک بلوک شدند و در ادامه یک پایگاه داده زنجیره بلوکی که به‌طور خودمختار مدیریت می‌شد و از یک شبکه نظیر به نظیر و یک سرور زمان‌بندی توزیع شده ‌استفاده می‌کرد را ایجاد کردند. این فناوری به تدریج تکامل پیدا کرد، به‌طوری که امروزه شاهد هستیم که رمزارزهای دیجیتالی زیادی بر پایه این فناوری ایجاد شده‌اند. با توجه به اهمیتی که درخت‌ها در دنیای دیجیتال دارند در این مقاله تصمیم گرفتیم به معرفی پرکاربردترین درخت‌ها بپردازیم. درخت‌هایی که برای حل بیشتر مشکلات از آن‌ها استفاده می‌شود. 

درخت 2-3

درخت 2-3 یک نوع درخت جست‌وجوی خودمتوازن است. درخت‌های جستجوی دودویی ممکن است با درج‌ها و حذف‌های گوناگون، حالت توازن خود را از دست بدهند. حالتی را در نظر بگیرید که یک درخت دودویی جست‌وجو دارید و n داده را که اتفاقا از کوچک به بزرگ مرتب هستند به ترتیب در آن درج می‌کنید. در این حالت، این درخت به یک فهرست پیوندی تبدیل می‌شود که جست‌وجو در آن از مرتبه (O(n است و گذشته از این که مزیت استفاده از درخت دودویی جستجو از بین رفته، مقدار زیادی حافظه هم با اختصاص دادن به اشاره‌گرهای تهی از دست می‌رود. پیاده‌سازی توابع درج و حذف درخت 2-3 به گونه‌ای است که این درخت طی درج‌ها و حذف‌ها به صورت متوازن باقی می‌ماند. درخت 2-3 سه نوع گره به نام‌های گره برگ که فقط یک مقدار دارد، گره 2 و گره 3 دارد. در گره 2، X مقدار گره، L زیردرخت سمت چپ و R زیردرخت راست گره است. هر گره 2 باید خصوصیات زیر را داشته باشد:

• هر مقدار در L باید کوچک‌تر از X باشد.
• هر مقدار در R باید بزرگ‌تر از X باشد.
• طول مسیرها از ریشه به برگ‌های هر یک از زیردرخت‌ها باید یکسان باشد.

در گره 3، X مقدار گره، L زیردرخت سمت چپ، M زیردرخت میانی و R زیردرخت راست گره است. هر گره 3 باید خصوصیات زیر را داشته باشد:

• هر مقدار در L باید کوچک‌تر از X باشد.
• هر مقدار در R باید بزرگ‌تر از X و کوچک‌تر از  Y باشد.
• هر مقدار در R باید بزرگ‌تر از Y باشد.
• طول مسیرها از ریشه به برگ‌های هریک از زیردرخت‌ها باید یکسان باشد.

باید توجه داشت که همه مقادیر در گره‌های برگ وجود دارند و گره‌های داخلی فقط برای هدایت جست‌وجو ایجاد شده‌اند. هر گره داخلی یک گره3 (با دو یا سه فرزند) است که مقدار X آن برابر با کوچک‌ترین مقدار موجود در زیردرخت دوم و مقدار Y آن (در صورت وجود) برابر با کوچک‌ترین مقدار موجود در زیردرخت سوم است.

شکل 1

درخت پیشوندی

Trie که به آن درخت پیشوندی (Prefix Tree) گفته می‌شود برای مسائل مرتبط با رشته‌ها (Strings) استفاده می‌شود. درخت‌های پیشوندی امکان بازیابی سریع را فراهم می‌کند و بیشتر برای جست‌وجوی کلمات در لغت‌نامه‌ها، پیشنهاد خودکار در موتورهای جست‌وجو و حتا مسیریابی آی‌پی استفاده می‌شوند. شکل 1 عملکرد این درخت را نشان می‌دهد. همان‌گونه که مشاهده می‌کنید، کلمات به‌شکل بالا به پایین در این درخت ذخیره‌ می‌شوند. در شکل فوق گره‌های سبز رنگ p،s و r نشانگر حروف پایان در واژگان top، thus و their هستند. از نکات مهمی که باید درباره درخت‌های پیشوند به آن‌ها دقت کنید، نحوه محاسبه تعداد کل کلمه‌ها در درخت پیشوندی، نمایش تمامی کلمات ذخیره شده در درخت پیشوندی، مرتب‌سازی عناصر یک آرایه با استفاده از درخت پیشوندی، شکل‌دهی کلماتی که درون یک لغت‌نامه قرار دارند و ساخت لغت‌نامه T9 است. 

درخت پسوندی

درخت پسوندی یک ترای (Trie) شامل پسوندهای یک رشته‌ داده شده به عنوان کلید و مکان آن‌ها در رشته به عنوان مقدار است. درخت پسوندی برای یک رشته S، درختی است که یال‌های آن با رشته‌هایی برچسب خورده‌اند، به‌طوری که هر پسوند S، متناظر با یک مسیر از ریشه درخت به یک برگ است، بنابراین، این درخت، یک درخت مبنا برای پسوندهای S است. ساخت چنین درختی برای رشته S به زمان و فضای خطی بر حسب طول S نیاز دارد. وقتی این درخت ساخته شود، عملیات رشته‌ای، مانند یافتن یک زیررشته در S، یافتن یک زیررشته با یک تعداد مجاز مشخص شده برای خطاها، یافتن تطابق‌ها برای یک الگوی عبارت باقاعده و غیره می‌توانند به سرعت انجام شوند. 

درخت جستجوی دودودیی

درخت جستجوی دودویی (Binary search tree) که گاهی اوقات درخت دودویی مرتب نامیده می‌شود، یک ساختار داده‌ای است و نوعی درخت دودویی است. یک درخت باینری نوعی ساختار داده برای ذخیره کردن داده‌هایی مثل اعداد است. درخت جست‌وجوی دودویی اجازه انجام کارهایی مثل جست‌وجوی یک عدد، اضافه و حذف آن عدد را سرعت بیشتری ارایه می‌کند. علاوه بر این، اجازه پیاده‌سازی مجموعه‌های پویا و جداول جست‌و‌جو را می‌دهد. ترتیب گره‌ها در درخت جست‌وجوی دودویی به صورتی است که در هر مقایسه نیمی از درخت باقی مانده بررسی نمی‌شود. بنابراین زمان جست‌وجوی درخت متناسب با لگاریتم تعداد عددهای ذخیره شده در درخت است. این زمان بسیار کمتر از زمان جست‌وجوی خطی در یک آرایه مرتب نشده، اما کندتر از انجام عملیات درهم‌سازی است. به‌طور معمول، درخت جست‌وجوی دودویی از تعدادی گره تشکیل شده که هر گره دارای یک کلید است. کلیدها منحصربه‌فرد هستند و در درخت کلید تکراری وجود ندارد.

تمام کلیدهایی که در زیردرخت سمت چپ واقع شده‌اند، کوچک‌تر از کلید گره ریشه هستند.

تمام کلیدهایی که در زیردرخت سمت راست واقع شده‌اند، بزرگ‌تر از کلید گره ریشه هستند.

زیردرخت سمت راست و زیردرخت سمت چپ خود درختان جست‌وجوی دودویی هستند.

درخت جست‌وجوی دودویی خود-متوازن

یک درخت درخت جستجوی دودویی خود-متوازن می‌تواند هر درخت جست‌وجوی دودویی گره‌محور باشد که به‌طور خودکار ارتفاعش را (حداکثر تعداد مراحل زیر ریشه) در درج و حذف عنصر دلخواه، کوچک نگه می‌دارد. این ساختارها اجراهای موثری برای فهرست‌‌های مرتب تغییر ناپذیر به وجود می‌آورند و می‌توانند به عنوان نوع داده انتزاعی مثل آرایه انجمنی، صف‌ اولویت‌دار و مجموعه‌ها استفاده شود. درخت‌های جست‌وجوی دودویی خود-متوازن به‌طور معمول می‌توانند در ساخت و نگهداری فهرست‌های مرتب شده ‌استفاده شوند. 

درخت جست‌وجوی سه‌تایی

درخت جست‌وجوی سه‌تایی نوعی درخت پیشوندی است، با این تفاوت که گره‌ها در حالت مشابه با درخت جست‌وجوی دودویی قرار گرفته‌اند، اما دارای سه فرزند هستند. مثل تمام درخت‌های پیشوندی، یک درخت جست‌وجوی سه‌تایی به عنوان داده ساختار آرایه انجمنی با توانایی جست‌وجوی رشته استفاده شود. از کاربردهای متداول درخت جست‌وجوی سه‌تایی می‌توان به غلط‌یاب و تکمیل خودکار اشاره کرد. مثل درخت دودویی که هر گره آن دارای یک مقدار و دو اشاره‌گر به زیردرختان‌اش است، هر گره از یک درخت جست‌وجوی سه‌تایی شامل یک کاراکتر و سه اشاره‌گر به زیر درخت‌های اول، دوم و زیردرخت سوم است که با نام‌های فرزند کوچکتر، فرزند مساوی و فرزند بزرگتر شناخته می‌شوند. یک گره می‌تواند اشاره‌گری به گره پدرش داشته باشد یا شاخصی که مشخص کند آیا به آخر کلمه رسیدیم یا نه. اشاره‌گر فرزند کوچکتر به گره‌ای دارای کاراکتر کوچ‌کتر از پدرش اشاره می‌کند. علاوه بر این، اشاره‌گر فرزند بزرگ‌تر به گره‌ای دارای کاراکتر بزرگ‌تر از پدرش اشاره می‌کند، اما اشاره‌گر فرزند مساوی به گره‌ای دارای کاراکتر بعدی در کلمه اشاره می‌کند. 

درخت دودویی

یک درخت دودویی یک ساختمان داده‌ درختی است که در آن هر گره حداکثر دو گره فرزند دارد که فرزندان راست و چپ نامیده می‌شوند. در درخت دودویی، درجه هر گره حداکثر می‌تواند دو باشد. درخت‌های دودویی برای پیاده‌سازی درخت جست‌وجوی دودویی و انبوه دودویی و برای جست‌وجوی کارآمد و مرتب‌سازی استفاده می‌شود. درخت دودویی یک حالت خاص از یک درخت kتایی است، که در آن k برابر ۲ است.

درخت دودویی بهینه

درخت دودویی جست‌وجوی بهینه یک نوع درخت دودویی جست‌وجو است. اگر از قبل بدانیم چه عناصری قرار است در درخت درج شود و احتمال آن‌که هر کدام از این عناصر مورد جست‌وجو قرار گیرند را بدانیم، می‌توانیم شکل بهینه‌تری از درخت دودویی جست‌وجو را ایجاد کنیم. دو روش برای بهینه‌تر کردن درخت دودویی جست‌وجو وجود دارد، یکی ایجاد یک درخت دودویی جست‌وجوی متوازن و دیگری ایجاد درخت دودویی جست‌وجوی بهینه با محاسبه احتمال دسترسی به هر کدام از عناصر. اگر داده‌ها از قبل آماده باشند، می‌توانیم آن‌ها را به گونه‌ای در درخت دودویی جست‌وجو قرار دهیم تا درختی متوازن ایجاد شود. در چنین شرایطی، با داشتن یک درخت دودویی جست‌وجو که متوازن است، در بدترین حالت، هزینه زمانی برابر با (O(lg n است. 

درخت دودویی نخی

در یک درخت دودویی، تعداد اتصالات تهی، بیشتر از تعداد اتصالات غیرتهی است. در یک درخت دودویی از کل اتصالات یعنی 2n، تعداد n+1 اتصال تهی است. از این اتصالات تهی می‌توان برای ارتباط با دیگر گره‌های درخت استفاده کرد. در درختی که اتصالات تهی آن به این شک استفاده شده‌، درخت دودویی ریسمان‌کشی شده (Threaded binary tree) نامیده می‌شود. یک درخت دودویی را می‌توان به چند روش ریسمان‌کشی کرد. این ریسمان‌کشی بسته به روش پیمایش درخت دارد. درخت دودویی نخ‌کشی شده اجازه پیمایش مقادیر در درخت دودویی به روش پیمایش خطی، سریعتر از پیمایش بازگشتی درخت به صورت میانوندی را می‌دهد. علاوه بر این، پیدا کردن والد یک گره در یک درخت دودویی نخی، بدون استفاده از اشاره‌گرهای والد یا بدون استفاده از پشته هم امکان‌پذیر است، هر چند که این کار کمی آهسته است. این قابلیت وقتی مفید است که فضای پشته اندک باشد یا وقتی که پشته اشاره‌گرهای والد غیرقابل دسترس باشد. 

درخت سرخ سیاه

درخت قرمز-سیاه بلوک، یک نوع درخت جستجوی دودویی خود-متوازن است. درخت سرخ‌سیاه اولین بار در دهه 70 میلادی توسط رودولف بایر درخت دودویی B متقارن نامیده شد، اما بعدها به‌نام درخت سرخ سیاه شهرت پیدا کرد. در مقایسه با درخت‌هایی که اشاره کردیم، درخت سرخ سیاه ساختار پیچیده‌ای دارد، با این حال در بدترین شرایط سرعت زیادی دارد. به بیان دقیق‌تر، زمان جست‌وجو، حذف و درج برای این درخت مانند O(log(n) که n تعداد گره‌های موجود در درخت است. 

مزیت عمده این ساختمان داده نسبت به درخت AVL این است که اعمال درج و حذف با تنها یک بار پیمایش درخت از بالا به پایین و تغییر رنگ گره‌ها انجام می‌شوند و در نتیجه پیاده‌سازی این درخت از درخت AVL ساده‌تر است. درختی که هر گره با یکی از دو رنگ سیاه یا قرمز رنگ‌آمیزی می‌شود، ریشه همیشه به رنگ سیاه است، اگر گره‌ای قرمز است و فرزندان آن سیاه هستند، تمامی مسیرها از یک گره به برگ‌ها (گره‌های null) تعداد مساوی گره سیاه دارند و تمامی برگ‌ها سیاه هستند (برگ گره‌ای است که فرزندی نداشته باشد گره‌ تهی است) درخت سرخ سیاه نامیده می‌شود. 

درخت کی دی

درخت کی‌دی (k-d tree) برای سازمان‌دهی نقاط در فضای k-بعدی استفاده می‌شود و بیشتر یک تعمیم از درخت دودویی جست‌و‌جو است. این درخت، یک ساختار داده مفید برای کاربردهایی مثل جست‌وجوهایی است که شامل کلید واژه‌های جست‌وجوی چند‌بعدی هستند. در این ساختار داده‌ای، هر گره آن یک نقطه K بعدی است و هر گره غیر برگ را می‌توان به عنوان یک مولد جداکننده که فضا را به دو قسمت تقسیم می‌کند توصیف کرد.